Угол 1 10 сколько градусов: Таблица конусов
Содержание
Калькулятор угла уклона пандуса
Калькулятор для пандуса
В соответствии с СП 59.13330.2016 «Доступность зданий и сооружений для маломобильных групп населения. Актуализированная редакция СНиП 35-01-2001» «Максимальная высота одного подъема (марша) пандуса не должна превышать 0,45 м при уклоне не более 1:20 (5%). При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 (10%)».
| Соотношение | Проценты | Градусы |
| 1:20 | 5% | 2,9° |
| 1:12 | 8% | 4,8° |
| 1:10 | 10% | 5,7° |
Введите параметры будущего пандуса, исходя из данных объекта. Параметры необходимо вводить в милиметрах. Нажмите кнопку «рассчитать». Длина наклонной площадки в рассчитывается в милиметрах. Также Вы получите рекомендации относительно параметров, которые у Вас получились.
Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2016 «Доступность зданий и сооружений для маломобильных групп населения»
При высоте марша до 800 мм — мах угол 2,86°
При высоте марша до 200 мм — мах угол 5,71°
Для временных конструкций
при высоте марша до 800 мм — мах угол 4,76°.
Пандус – это устройство для адаптации социально-значимых объектов и открытых пространств: вход в здание, сопровождение лестницы, пешеходный переход и т.д. Пандус необходим, чтобы сделать жизнь маломобильных групп населения комфортнее: пожилые люди, с коляской или тяжелой поклажей, с костылями после травм, инвалиды-колясочники.
Активное развитие и продвижение федеральной программы «Доступная среда» сподвигло многие организации установить пандусы на входной группе. Однако зачастую это делается либо для галочки, либо организациями, не владеющими навыками и знаниями существующих нормативов. Поэтому не всегда готовое изделие соответствует государственным стандартам. Как результат — недоступность для людей с ограничениями.
Как результат — недоступность для людей с ограничениями.
Нормативы для пандусов 2018
По нормативам СП 59.13330.2016 (с учетом вступивших в силу изменений 15 Мая 2017 года) пандус должен иметь следующие характеристики:
Список документации, рекомендуемой к ознакомлению:
- СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов.
- ГОСТ Р 51261-2017 содержит технические требования к стационарным опорным устройствам.
- СП 30-102-99 содержит требования к входной площадке.
- СП 59.13330.2016 содержит предписания по доступности зданий и сооружений для маломобильных групп населения
Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем /спуск получается в разы выше.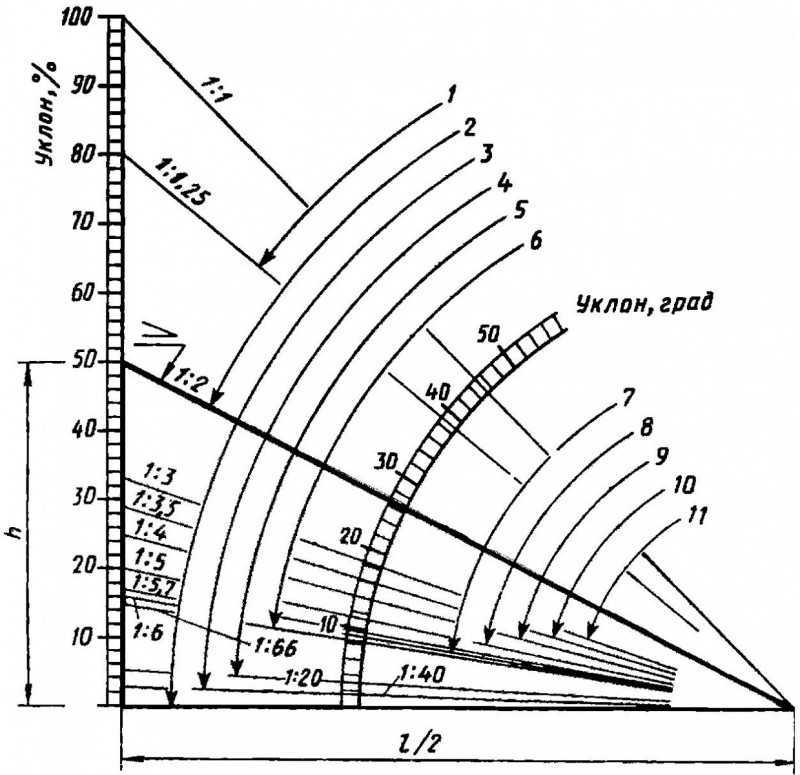 Угол наклона — это соотношение длины к высоте подъема.
Угол наклона — это соотношение длины к высоте подъема.
Запомните! При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.
Справка! В ряде некоторых случаев допускается небольшое увеличение угла наклона пандуса:
- При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
- Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
- Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать разворотную площадку или площадку отдыха.
- Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
- Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.

- Поверхность пандуса должна быть нескользкой текстурой.
- Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.
Поручни для пандуса
- В начале и конце поручни должны быть длиннее на 300 мм и иметь закруглённую форму.
- Верхний поручень расположен на высоте 900 мм.
- Расстояние между поручнями 900-1000 мм.
- Перила должны быть круглого сечения с диаметром от 30 до 50 мм.
- Начало и конец маркируются предупредительными полосами.
- Нижний поручень должен быть на высоте 700 мм.
- По продольным краям марша пандуса следует устанавливать бортики высотой не менее 0,05 м.
- Покрытие пандуса должно обладать противоскользящим эффектом.
- Минимальное расстояние от гладкой стены 45 мм, от неровной 60 мм.
- Поручни с внутренней стороны не должны прерываться.
- Поручни изготавливаются из металла и устанавливаются с обеих сторон наклонной площадки.

Если пандус изначально соответствует всем строительным параметрам, то его можно оснастить необходимыми дополнительными устройствами при их отсутствии:
- Опорными поручнями. Расстояние между поручнями пандуса одностороннего движения должно быть в пределах 0,9-1,0 м, чтобы инвалид-колясочник мог на них подтянуться. Также для удобства и безопасности хвата поручни должны иметь закругленную форму и выступать на 300 мм от края.
- Контрастной тактильной разметкой (для незрячих и слабовидящих людей). Разметкой следует обозначать сами поручни и подстилающую поверхность. С внутренней стороны поручней можно приклеить тактильные наклейки для обозначения начала и конца препятствия.
Если пандус изначально не соответствует конструкторским параметрам в соответствии со сводами правил, то его следует демонтировать, а на его месте организовать доступный пандус.
Вопросы по адаптации
Автопарковка для МГН
Адаптация тротуаров для незрячих
Адаптация лестниц для МГН
Адаптация входной группы
Адаптация холла в помещении
Адаптация санузела для незрячих
Адаптация лифтов для МГН
НАШЕ ПРЕИМУЩЕСТВО — ДОЛГОЛЕТНИЙ ОПЫТ и КАЧЕСТВО!
Что такое конусность 1 10?
Что такое конусность 1 10?
Конусность, как правило, выражается в отношении двух чисел например конусность 1:10 означает что высота полного конуса в 10 раз больше диаметра основания. Также конусность может задаваться углом вершины конуса (α). Половина угла вершины конуса называется уклоном конуса (α/2).
Также конусность может задаваться углом вершины конуса (α). Половина угла вершины конуса называется уклоном конуса (α/2).
Как узнать конусность?
Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте.
Какой знак определяет конусность поверхности?
conus – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов. ». Знак конусности с размерными числами наносятся над осевой линией или на полке линии-выноски. Отношение диаметра основания конуса к его высоте называется конусностью.
Сколько градусов в конус Морзе?
Морзе приблизительно в 1864 году. Конус Морзе подразделяется на восемь размеров, от КМ0 до КМ7 (англ. Morse taper, MT0-MT7, нем. Morsekegel, MK0-MK7). Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26» до 3°00’52», уклон конуса от 1°25’43» до 1°30’26») в зависимости от типоразмера.
Morsekegel, MK0-MK7). Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26» до 3°00’52», уклон конуса от 1°25’43» до 1°30’26») в зависимости от типоразмера.
Как рассчитать конус Морзе?
Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h. Обозначение конусности на чертежах.
Как рассчитать конус формула?
Формулы для вычисления объема конуса: 1) Объем конуса равен одной трети произведения площади основания на высоту. 2) Объем конуса равен одной трети произведения числа пи (3.
Какой конус в сверлильном патроне?
Существуют различные стандарты крепления сверлильных патронов к станку: конические хвостовики, посадка на резьбу и т. п. Стоит отметить, что наивысшей точностью посадки, позволяющей минимизировать биение, отличаются сверлильные патроны с конусом Морзе (самые популярные размеры — В16 и В18).
Стоит отметить, что наивысшей точностью посадки, позволяющей минимизировать биение, отличаются сверлильные патроны с конусом Морзе (самые популярные размеры — В16 и В18).
Какой угол у конуса Морзе 2?
| Конусность | Угол конуса | Обозначение |
|---|---|---|
| 1:20,020=0,04995 | 2 градуса 51 минута 41 секунда | Конус Морзе 2 |
| 1:19,922=0,05020 | 2 градуса 52 минуты 32 секунды | Конус Морзе 3 |
| 1:19,254=0,05194 | 2 градуса 58 минут 31 секунда | Конус Морзе 4 |
| 1:19,002=0,05263 | 3 градуса 00 минут 53 секунды | Конус Морзе 5 |
Какие бывают виды конуса?
Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания. Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.
Для чего нужен конус Морзе?
Конус инструментальный — конический хвостовик инструмента (сверло, зенкер, фреза, развёртка) и коническое отверстие соответствующего размера (гнездо) в шпинделе или задней бабке станка. Предназначено для быстрой смены инструмента с высокой точностью центрирования и надёжностью.
Где используется конус?
Знания о конусе широко применяются в жизни — в быту, на производстве, в науке. Например, в быту мы часто используем вёдра, имеющие форму усечённого конуса, служащие нам ёмкостью для различных жидкостей и сыпучих веществ. Наши растения, благоприятно развиваются в цветочных горшках.
Как называть конус?
Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Как называется конус без конца?
Усеченный конус Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.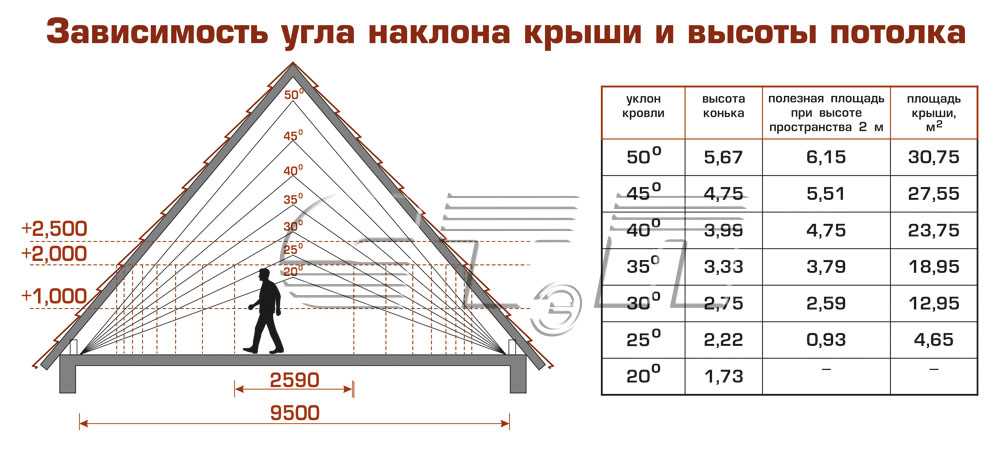 Обычно под усеченным конусом имеется ввиду часть прямого кругового конуса.
Обычно под усеченным конусом имеется ввиду часть прямого кругового конуса.
Чем отличается полный конус от усеченного?
Круговой конус — конус, основание которого является кругом. … Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием. Равносторонний конус — конус вращения, образующая которого равна диаметру основания.
Что называется высотой усеченного конуса?
Высотой усеченного конуса называют расстояние между плоскостями расстояние между плоскостями оснований усеченного конуса.
Что такое развертка конуса?
Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью. Варианты построения развертки: … Усеченный конус
Что такое круговой конус?
Конусом ( прямым круговым конусом ) называется тело, состоящее из круга ( основания конуса ), точки, не лежащей в плоскости этого круга ( вершины конуса ), и всех отрезков, соединяющих вершину конуса с точками основания. … Отрезки называют образующими конической поверхности, а кривую – направляющей.
… Отрезки называют образующими конической поверхности, а кривую – направляющей.
Что называется высотой конуса?
Отрезки, соединяющие вершину конуса с точками его основания, называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость его основания, а также длина этого перпендикуляра.
Сколько осевых сечений имеет конус?
Представляет из себя прямоугольник, две стороны которого – образующие цилиндра, а две другие – параллельные хорды верхнего и нижнего основания цилиндра. 9 Виды сечений конуса Осевое сечение конуса. Представляет из себя треугольник, две стороны которого – образующие конуса, а третья сторона – диаметр основания конуса.
Как получается конус?
Конус называется круговым, если в его основании лежит круг. … Прямой круговой конус образуется при вращении прямоугольного треугольника вокруг его катета. Прямой круговой конус определяется радиусом основания R и высотой H (или радиусом основания R и образующей m).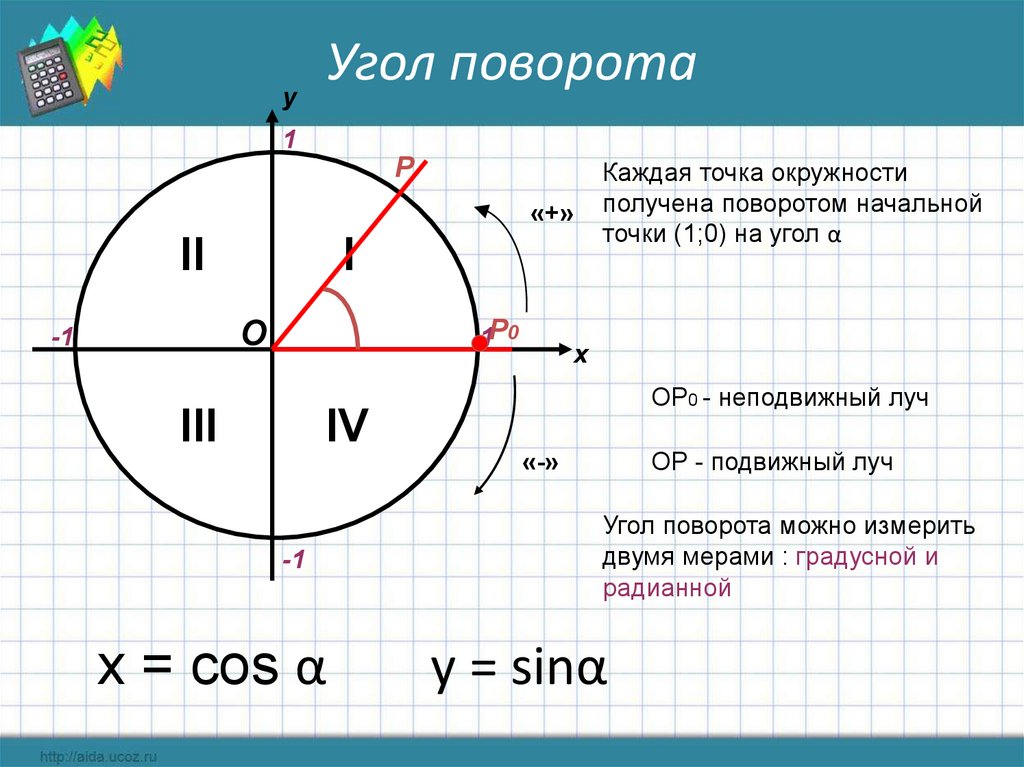
Что такое вершина конуса?
вершина конуса — Точка пересечения образующей конуса с осью. 1 вершина; 2 образующая; 3 основание; 4 коническая поверхность; 5 ось [ГОСТ (CT СЭВ 1779 79)] Тематики нормы взаимозаменяемости Обобщающие термины элементы конуса EN cone point DE Kegelspitze… …
Что такое конус нарастания?
Конус нарастания Конус нарастания, закругленно-конусовидная верхушка растущего осевого органа (стебля, корня) растения, состоящая из образовательной ткани (меристемы). … происходит рост растений.
Кто придумал конус?
Чарльз Рудбэйкер
Сколько основ имеет конус?
у конуса может быть одна из четырех основ: круг, парабола, эллипс и гипербола.
Сколько осей симметрии имеет конус?
Конус также имеет ось симметрии, причём, поскольку число поворотов конуса вокруг своей оси симметрии, приводящих к «самосовмещению» бесконечно, то говорят, что конус имеет ось симметрии типа L8.
Как можно получить усеченный конус?
Усеченный конус можно получить и как тело вращения. Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.
Как может быть вращением получен усеченный конус?
Все образующие усеченного конуса равны друг другу. Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Как найти площадь осевого сечения?
Формула для расчета площади основания конуса:
- S = π * d 2 / 4, где d — диаметр конуса. Формула для расчета площади осевого сечения конуса:
- S = d * h / 2, где d — диаметр конуса; h — высота конуса. …
- S = a * h / 2, где a — хорда основания конуса; h — высота конуса.
Что представляет собой осевое сечение усеченного конуса?
Осевым сечением усеченного конуса является равнобедренная трапеция, высота которой равна диаметру большего основания; радиусы основания равны 18 см и 10 см.
Конвертер окружности 1/10 в градусы
Введите значение
Введите значение
Вывод
Вывод
Сколько градусов в окружности 1/10?
Ответ: один Окружность 1/10 равна 36 градусам. Воспользуйтесь нашим онлайн-калькулятором перевода единиц измерения, чтобы перевести единицы из 1/10 окружности в градусы. Просто введите значение 1 в Agate Line и посмотрите результат в градусах.
Как преобразовать окружность 1/10 в градусы (окружность в градусы)
Используя наш инструмент преобразования окружности 1/10 в градусы, вы знаете, что одна окружность 1/10 эквивалентна 36 градусам. Следовательно, чтобы преобразовать окружность 1/10 в градусы, нам просто нужно умножить число на 36. Для этого мы будем использовать очень простую формулу преобразования окружности 1/10 в градусы. См. приведенный ниже пример расчета.
Преобразовать 1 окружность 1/10 в градусы ⇒ 1 окружность 1/10 = 1 × 36 = 36 градусов
Что такое единица измерения окружности 1/10?
Окружность 1/10 — это единица измерения угла. Окружность 1/10 равна 36 градусам.
Окружность 1/10 равна 36 градусам.
Что означает круг 1/10?
Символом Круга 1/10 является круг. Это означает, что вы также можете записать один круг 1/10 как 1 круг.
Что такое градус?
Градус — единица измерения плоского угла. Один полный оборот считается 360 градусов. Степень также упоминается как степень дуги, степень дуги или степень дуги. Конкретная причина выбора градуса в качестве единицы поворотов и углов довольно неясна, но, согласно историческим фактам, 360 — это примерное количество дней в году.
Что означает степень?
Символ градуса — град. Это означает, что вы также можете записать один градус как 1 градус.
Circle 1/10 to Degree Conversion Table
| Circle 1/10 [circle] | Degree [deg] |
|---|---|
| 1 | 36 |
| 2 | 72 |
| 3 | 108 |
| 4 | 144 |
| 5 | 180 |
| 6 | 216 |
| 7 | 252 |
| 8 | 288 |
| 9 | 324 |
| 10 | 360 |
| 100 | 3600 |
| 1000 | 36000 |
Круг 1/10 до других единиц.
 0048
0048
 Окружность 1/4 равна
Окружность 1/4 равнаПреобразовать круг 1/10 в другие угол
Октятный к Radian
404 к Октяну Октансу к Quadrant
.0003
Измерение углов
Измерение углов
Понятие угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.
Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Градусы могут быть далее разделены на минуты и секунды, но это деление уже не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутой. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых 9.0291 секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часов на минуты и секунды времени. |
Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5°.
Когда один угол начерчен на плоскости xy для анализа, мы нарисуем его за стандартная позиция с вершиной в начале координат (0,0), одна сторона угла вдоль оси x , а другая сторона над осью x .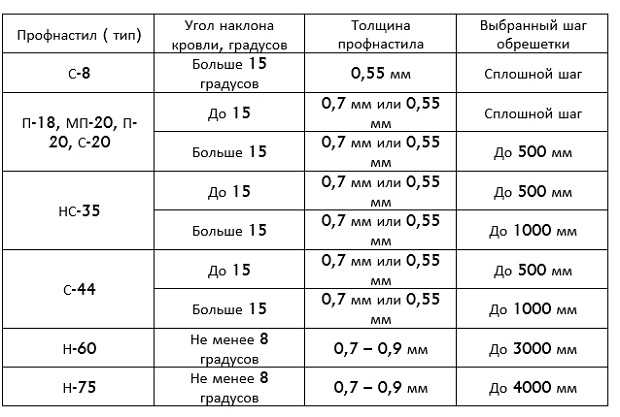
радиан
Другой распространенной единицей измерения углов являются радианы. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радианам. Следовательно, а также Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор. |
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге « Элементы алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной на единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.
Например, Леонард Эйлер (1707–1783) в своей книге « Элементы алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной на единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.
e iθ = cos θ + i sin θ
где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.
Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.
Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах. Поскольку площадь всего круга равна πr 2 , а сектор относится ко всему кругу как угол θ к 2 π , поэтому
Поскольку площадь всего круга равна πr 2 , а сектор относится ко всему кругу как угол θ к 2 π , поэтому
Углы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дано в виде π 9029.2 . Его можно, конечно, представить в десятичном виде, но радианы часто появляются с коэффициентом π .
.
| Уголок | градусов | радиан |
|---|---|---|
| 90° | № /2 | |
| 60° | № /3 | |
| 45° | № /4 | |
| 30° | № /6 |
Упражнения
Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г.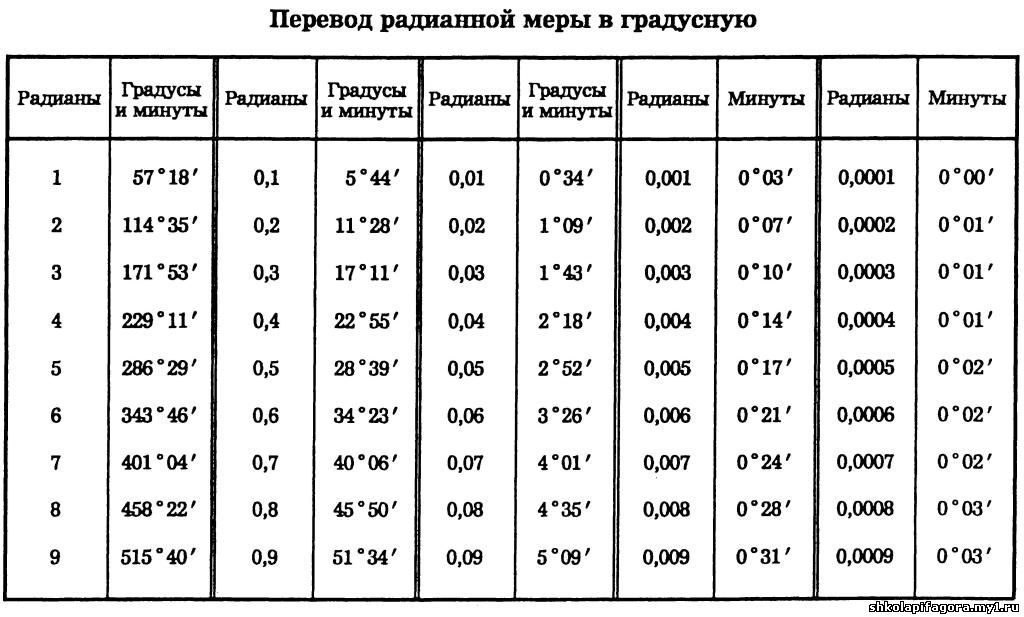 Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минут, радиус от центральной линии пути составляет 2100 футов.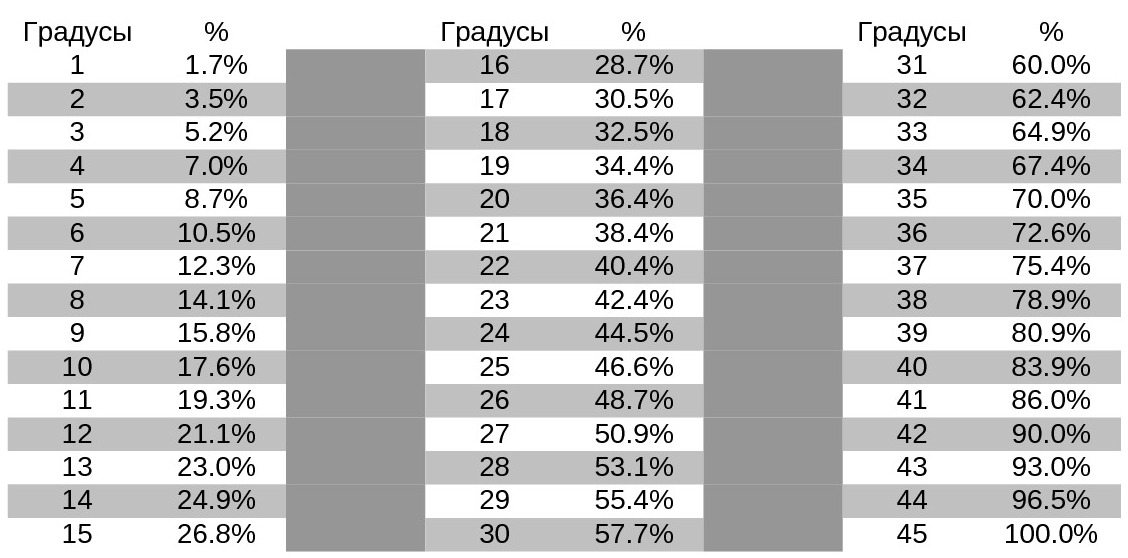 Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. Насколько изменится широта, если пройти на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
23. Известно, что воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?
Советы
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы. Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.
2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535
радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть
2102,5 a – 1997,5 a , что равно 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
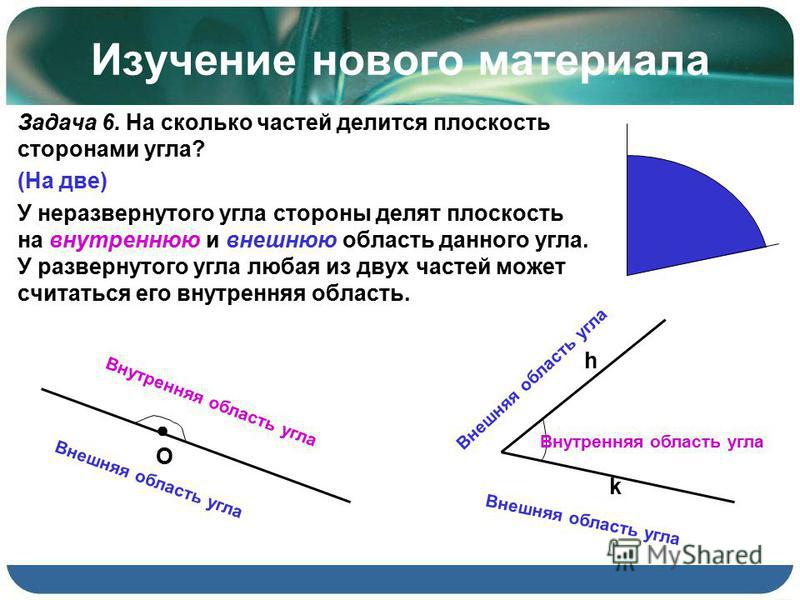

 Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы.
Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы.