Вычисление площадей плоских фигур с помощью интеграла. Расчет площади фигур

Формулы площадей всех основных фигур

1. Формула площади равнобедренной трапеции через стороны и угол

b - верхнее основание

a - нижнее основание

c - равные боковые стороны

α - угол при нижнем основании

 

Формула площади равнобедренной трапеции через стороны, (S):

 

Формула площади равнобедренной трапеции через стороны и угол, (S):

 

 

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R - радиус вписанной окружности

D - диаметр вписанной окружности

O - центр вписанной окружности

H - высота трапеции

α, β - углы трапеции

 

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

 

 

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d - диагональ трапеции

α, β - углы между диагоналями

 

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

 

 

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m - средняя линия трапеции

c - боковая сторона

α, β - углы при основании

 

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

 

 

5. Формула площади равнобедренной трапеции через основания и высоту

b - верхнее основание

a - нижнее основание

h - высота трапеции

 

Формула площади равнобедренной трапеции через основания и высоту, (S):

 

www-formula.ru

Формула вычисления площади для всех геометрических фигур

Стандартное обозначение площади - S

Площадь

Пусть длина стороны квадрата равна a, тогда формул квадрата:

S = a ⋅ a = a2

Прямоугльник

Пусть длины сторон прямоугольника равны a и b

S = a ⋅ b

Параллелограмм

Пусть длины сторон параллелограмма равны a и b и ha это высота на сторону a, и hb это высота на сторону bФормула площади параллелограмма:

S = a ⋅ ha = b ⋅ hb

Трапеция

Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude). Тогда формула площади:

$S = \frac{(a + b)\cdot h}{2}$

Площадь круга

$P = \pi\cdot r^2$

$\pi=3,14$

Площадь прямоугольного треугольника

$S=\frac{a \cdot b}{2}$

$S=\frac{c \cdot h_c}{2}$

Площадь треугольника - калькулятор

Стороны треугольника:

Треугольник

ABC - треугольник

длина его сторон: a, b, c и длина его высот: ha, hb и hc.

S = ½(a ⋅ ha) = ½(b ⋅ hb) = ½(c ⋅ hc)

S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)

p = ½(a + b + c)

S = √p(p - a)(p - b)(p - c) - формула Герона

$S = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$

где R - радиус описанной окружности

Площадь параллелограмма(ромба)

$S = AB\cdot DE = BC \cdot DF$$S = AB \cdot AD \sin \alpha$$S = \frac12 AC \cdot BD \sin \gamma$

Площадь выпуклого четырехугольника

$S = \frac12 AC \cdot BD \sin \varphi $

Площадь правильного многоугольника

$S = \frac14 n\cdot a^2\cdot \text{ctg}(\frac{\pi}{n})$

n - число ребер(вершин).$\pi=3,14159265359$

www.math10.com

Вычисление площадей плоских фигур с помощью интеграла

На этом уроке будем учиться вычислять площади плоских фигур, которые ограничены осью абсцисс (Ox), отрезками прямых x = a, x = b и графиком непрерывной и неотрицательной функции y = f(x) для значений "икса", принадлежащих отрезку [a, b]. Такая фигура называется криволинейной трапецией. Боковые отрезки могут вырождаться в точки.

Площадь s этой криволинейной трапеции может быть вычислена по формуле

 (1).

Итак, определённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] (график функции расположен выше оси Ox) численно равен площади криволинейной трапеции с основанием [a, b], ограниченной сверху графиком функции y = f(x). В этом заключается геометрический смысл определённого интеграла. Рисунки таких фигур - в примерах.

Если же f(x) ≤ 0 (график функции расположен ниже оси Ox), то площадь криволинейной трапеции может быть вычислена по формуле

. (2)

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры - функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле

. (3)

Таким образом, вычисление площадей плоских фигур - одна из важнейших прикладных задач, в которой определённый интеграл находит наиболее плодотворное применение. Все мы изучали сведения из элементарной геометрии, которые позволяют вычислять площади прямолинейных фигур - прямоугольников, треугольников и многоугольников. Что же касается криволинейных фигур, то здесь для нахождения площади средств из элементарной геометрии уже недостаточно. Итак, к делу. Учимся применять то, что изложено в самом верху этой статьи.

Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).

Пример 1. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox) и прямыми x = 1, x = 3.

Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):

.

Пример 3. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox) и прямой x = 4.

Решение. Фигура, соответствующая условию задачи - криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку , по формуле (1) находим площадь криволинейной трапеции:

.

Пример 4. Найти площадь фигуры, ограниченной линиями , , и находящейся в 1-й четверти.

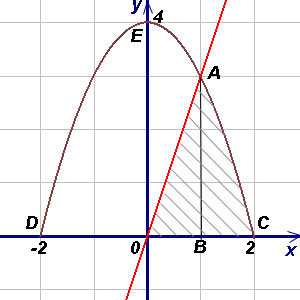
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим (абсциссу точки A) и (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим , (абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:

Пример 5. Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD и абсциссы A и B соответственно 1 и 2.

Решение. Выразим данное уравнение кривой через игрек: Площадь криволинейной трапеции находим по формуле (1):

.

Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).

Пример 7. Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.

Решение. Площадь данной фигуры можем найти по формуле (2):

.

Найдём отдельно каждое слагаемое:

.

.

Окончательно находим площадь:

.

Пример 8. Найти площадь фигуры, заключённой между параболой и кривой .

Решение. Выразим уравнения линий через игрек:

Площадь по формуле (2) получим как

,

где a и b - абсциссы точек A и B. Найдём их, решая совместно уравнения:

Отсюда

Окончательно находим площадь:

И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3). Первый из этих примеров предлагается решить самостоятельно, а затем можно посмотреть правильное решение.

Начало темы "Интеграл"

function-x.ru

Площади геометрических фигур / math5school.ru

	Треугольник		Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.
	Треугольник		Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
	Треугольник		Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон.
	Треугольник		Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла.
	Треугольник		Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов.
	Треугольник		Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника.
	Прямоугольный треугольник		Площадь прямоугольного треугольника равна половине произведения его катетов.
	Равнобедренный треугольник		Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания.
	Равносторонний треугольник		Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх.
	Равносторонний треугольник		Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх.
	Треугольник		Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности.
	Треугольник		Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов.
	Треугольник		Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник).
	Треугольник		Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника.
	Прямоугольник		Площадь прямоугольника равна произведению двух соседних его сторон.
	Квадрат		Площадь квадрата равна квадрату его стороны.
	Квадрат		Площадь квадрата равна половине квадрата его диагонали.
	Параллелограмм		Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
	Параллелограмм		Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними.
	Ромб		Площадь ромба равна произведению квадрата его стороны на синус одного из его углов.
	Ромб (дельтоид)		Площадь ромба (как и дельтоида) равна половине произведения его диагоналей.
	Трапеция		Площадь трапеции равна произведению полусуммы её оснований на высоту.
	Трапеция		Площадь трапеции равна произведению её средней линии на высоту.
	Выпуклый четырёхугольник		Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
	Вписанный четырёхугольник		Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон.
	Круг		Площадь круга равна произведению числа "пи" на квадрат радиуса.
	Круг		Площадь круга равна четверти произведения числа "пи" на квадрат диаметра.
	Круговой сектор	формулы для случаев градусной и радианной мер центральных углов	Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору.
	Круговое кольцо		Площадь кругового кольца равна произведению числа "пи" на разность квадратов внешнего и внутреннего радиусов.
	Круговое кольцо		Площадь кругового кольца равна четверти произведения числа "пи" на разность квадратов внешнего и внутреннего диаметров.
	Круговое кольцо		Площадь кругового кольца равна удвоенному произведению числа "пи", среднего радиуса кольца и его ширины.

math4school.ru

Калькулятор для расчета площади различных геометрических фигур

Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:

Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.

Полезные калькуляторы Конвертер едениц площади | Конвертер едениц длины

Расчет площади прямоугольника

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади треугольника

Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними

Вычислить

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади параллелограмма

Способ нахождения площади параллелограмма:По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними

Вычислить

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади правильного многоугольника

Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r

Вычислить

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади круга

Рассчитать площадь круга, если известен:

Вычислить

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади эллипса

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади сектора круга

Рассчитать площадь сектора круга, если известен:

r= ммсммкмфутярддюйммиля
θ= ммсммкмфутярддюйммиля град.рад.

Вычислить

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади трапеции

Способ нахождения площади треугольника: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d

 

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.

Метрические единицы измерения площади:
Квадратный метр, производная единица системы СИ 1 м2 =	1 са (сантиар)
Квадратный километр - 1 км2 =	1 000 000 м2
Гектар - 1 га =	10 000 м2
Ар (сотка) - 1 а =	100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м)
Квадратный дециметр, 100 дм2 =	1 м2;
Квадратный сантиметр, 10 000 см2 =	1 м2;
Квадратный миллиметр, 1 000 000 мм2 =	1 м2.

Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.

remont-otdelka-m.ru

Формулы площадей и объемов геометрических фигур

 

	Главная > Учебные материалы > Математика:  Формулы площадей и объемов геометрических фигур
	Репетитор: Васильев Алексей Александрович  Предметы: математика, физика, информатика, экономика.        Стоимость: 2000 руб / 90 мин.  Репетитор: Крюков Илья Хассанович  Предметы: математика, экономика, эконометрика, теория вероятностей.        Стоимость: 2000 руб / 90 мин.  Репетитор: Скрипаленко Михаил Михайлович  Предметы: математика (ЕГЭ), английский язык (GMAT, GRE (general), GRE subject test in maths, IELTS, TOEFL, BEC).        Стоимость: 1200 руб / 60 мин.  Репетитор: Матвеева Милада Андреевна  Предметы: русский язык, литература (ЕГЭ, ГИА).        Стоимость: 1200 руб / 60 мин.  Репетитор: Тверской Василий Борисович  Предметы: математика, физика.        Стоимость: 3500 руб / 90 мин.  Репетитор: Поздняков Андрей Александрович  Предметы: английский язык, (ЕГЭ). Подготовка к TOEFL и IELTS.        Стоимость: 2000 руб / 60 мин.  Репетитор: Ершикова Марина Львовна  Предметы: бухгалтерский учет (кроме банковского), налогообложение, аудит.        Стоимость: 1500 руб / 60 мин.
	Формулы площадей     1.Площадь многоугольника.    2.Площадь треугольника.     3.Площадь квадрата.     4.Площадь прямоугольника.    5.Площадь параллелограмма.     6.Площадь ромба.     7.Площадь трапеции.     8.Площадь четырехугольника.     9.Площадь круга.     10.Площадь кругового сектора.    11.Площадь эллипса. Формулы объемов     1.Объем куба.     2.Объем параллелепипеда.     3.Объем призмы.     4.Объем пирамиды.     5.Объем усеченной пирамиды.     6.Объем цилиндра.     7.Объем правильной треугольной пирамиды.     8.Объем конуса.     9.Объем усеченного конуса.     10.Объем тетраэдра.     11.Объем шара.     12.Объем шарового сегмента и сектора.   Примеры решений С1. Видео.
1 2 3 4 5 6 7 8
	Площадь многоугольника
	Рассчитать площадь многоугольника вписанного в круг и описанного около круга
	Площадь треугольника
Рассчитать площадь треугольника
	Площадь квадрата
	Рассчитать площадь квадрата
	Площадь прямоугольника
	Рассчитать площадь прямоугольника
	Площадь параллелограмма
	Рассчитать площадь параллелограмма
	Площадь ромба
	Рассчитать площадь ромба
	Площадь трапеции
	Рассчитать площадь трапеции
	Площадь четырехугольника
	Рассчитать площадь четырехугольника
	Площадь круга
	Рассчитать площадь круга, длину окружности
	Площадь кругового сектора, длина дуги
	Рассчитать площадь кругового сектора, длину дуги
	Площадь эллипса
	Рассчитать площадь эллипса
	Объем куба
	Рассчитать объем и площадь поверхности куба
	Объем параллелепипеда
	Рассчитать объем параллелепипеда
	Объем призмы
	Рассчитать объем призмы
	Объем пирамиды
	Рассчитать объем пирамиды
	Объем усеченной пирамиды
	Рассчитать объем усеченной пирамиды
	Объем цилиндра
	Рассчитать объем цилиндра
	Объем правильной треугольной пирамиды
	Рассчитать объем правильной треугольной пирамиды
	Объем конуса
	Рассчитать объем конуса
	Объем усеченного конуса
	Рассчитать объем усеченного конуса
	Объем тетраэдра
	Рассчитать объем тетраэдра
	Объем шара
	Рассчитать объем и площадь поверхности шара
	Объем шарового сегмента и сектора
	Рассчитать объем шарового сегмента
1 2 3 4 5 6 7 8

www.mathtask.ru

Расчет площади геометрических фигур | International Institute of Care to Buildings

СПРАВОЧНИКИ

 

 

Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

1-ая формула

S - площадь треугольника

a, b - длины 2-х сторон треугольника

С - угол между сторонами a и b

2-ая формула

S - площадь треугольника

a - длина стороны треугольника

h - длина высоты, опущенной на сторону a

3-ья формула

S - площадь треугольника

a, b, c - длины 3-х сторон треугольника

p - полупериметр треугольника

4-ая формула

S - площадь треугольника

r - радиус вписанной окружности

p - полупериметр треугольника

5-ая формула

S - площадь треугольника

a, b, c - длины 3-х сторон треугольника

R - радиус описанной окружности

См. также: Онлайн калькулятор для расчета площади треугольника.

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S - площадь квадрата

a - длина стороны квадрата

d - длина диагонали квадрата

См. также: Онлайн кальклятор для расчета площади квадрата.

Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S - площадь прямоугольника

a - длина 1-ой стороны прямоугольника

b - длина 2-ой стороны прямоугольника

См. также: Онлайн калькулятор для расчета площади прямоугольника.

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

S - площадь параллелограмма

a - длина основания

h - длина высоты

См. также: Онлайн калькулятор для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S - площадь трапеции

a - длина 1-ого основания

b - длина 2-ого основания

h - длина высоты трапеции

См. также: Онлайн калькулятор для расчета площади трапеции.

Формулы площади ромба:

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

S - площадь ромба

a - длина основания ромба

h - длина высоты ромба

d1 - длина 1-ой диагонали

d2 - длина 2-ой диагонали

См. также: Онлайн калькулятор для расчета площади ромба.

Формула площади круга:

1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

S - площадь круга

π - число пи (3.1415)

r - радиус круга

См. также: Онлайн калькулятор для расчета площади круга.

Формула площади эллипса:

1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).

S - площадь эллипса

π - число пи (3.1415)

a - длина большой полуоси

b - длина малой полуоси

См. также: Онлайн калькулятор для расчета площади эллипса.

 

 

 

miuz.org

---

• 
  Электронасос для отопления
• 
  Как правильно утеплить цоколь дома снаружи пенополистиролом
• 
  Отделка ванной деревом
• 
  Как сделать ленточный фундамент своими руками
• 
  Интерьер с камнем декоративным
• 
  Баня каркасная проект
• 
  Расключение электрощита в квартире
• 
  Утеплить балкон самостоятельно
• 
  Декоративная наружная штукатурка
• 
  Как шпаклевать дсп под обои
• 
  Как обшить в бане потолок вагонкой своими руками