Площадь по периметру калькулятор: Расчет площади прямоугольника по периметру
Содержание
Калькулятор вычисления периметра и площади геометрических фигур
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Круг
Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так. Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади. Длина окружности или периметр круга находятся по простой формуле:
Длина окружности или периметр круга находятся по простой формуле:
l = 2 pi × R,
где R – радиус фигуры.
Площадь круга рассчитывается согласно следующему выражению:
S = pi R2
Круги часто встречаются в реальной жизни. В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
Треугольник
Треугольник — первая гармоничная фигура на плоскости, ограниченная тремя отрезками. Свойства треугольника известны людям с античных времен: изучение фигуры стартовало в Древнем Египте и не завершено до сих пор.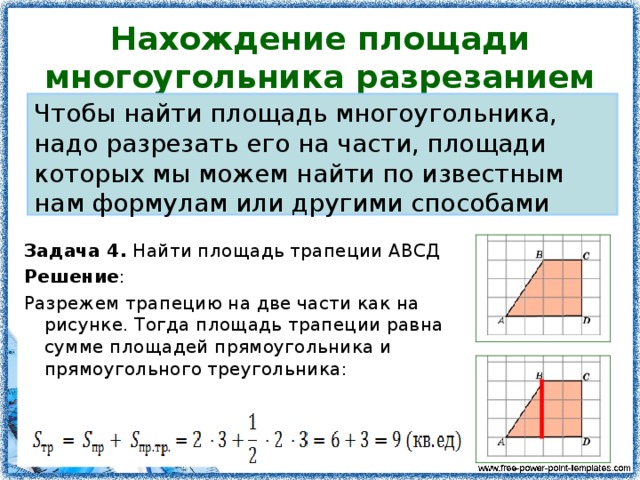 Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч. Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:
Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч. Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:
P = a + b + c,
где a, b, c – стороны.
Для вычисления площади треугольника используется 5 различных формул плюс нахождение площади через определенный интеграл. Самое простое выражение для вычисления площади:
S = 0,5 a × h,
где a — сторона треугольника, h — его высота.
Наш калькулятор позволяет отыскать площадь или периметр треугольника, зная разные комбинации нескольких параметров, таких как углы, стороны или радиусы связанных окружностей.
Треугольники не слишком распространены в реальной повседневности. В природе они практически не встречаются, за исключением кристаллических решеток некоторых молекул или формы ушей у рыси. А вот в технике, геометрии и прикладных науках треугольник — царь и бог. Наибольшее применение находит следующий тип фигуры.
Наибольшее применение находит следующий тип фигуры.
Прямоугольный треугольник
Прямоугольный треугольник — особая вариация фигуры, у которой две стороны обязательно образуют прямой угол. Эти стороны называются катетами, а противолежащая им сторона — гипотенузой. Соотношение катетов и гипотенузы лежит в основе евклидовой геометрии — эти соотношения определяются теоремой Пифагора. Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.
Формулы для вычисления периметра и площади прямоугольного треугольника ничем не отличаются от формул для обычных вариаций данной фигуры или вытекают из них.
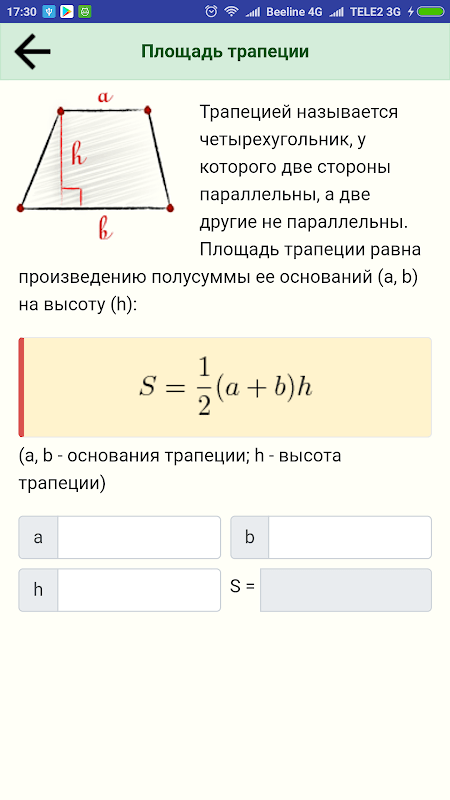
Трапеция
Трапеция, как и слово трапеза, по-гречески означают «стол». Это плоская фигура, ограниченная четырьмя прямыми, две из которых параллельны, а две — нет. По сути, это выпуклый четырехугольник, поэтому параллелограмм и прямоугольник считаются частными случаями трапеции.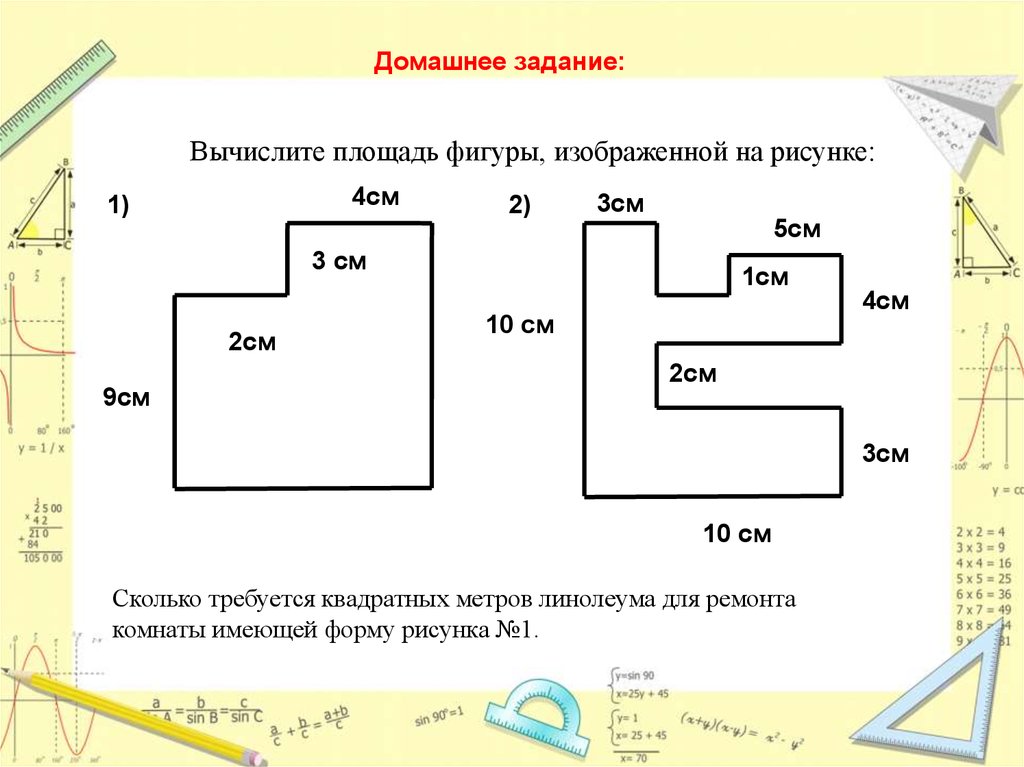 В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:
В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:
P = a + b + c + d,
a, b, c и d – стороны четырехугольника.
Площадь фигуры определяется как:
S = 0,5 (a + b) × h,
где a и b – параллельные стороны трапеции, h – высота.
Трапеция очень часто встречается в рукотворном мире. Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.
Параллелограмм
Параллелограмм — это элегантный четырехугольник, пары сторон которого параллельны друг другу. Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны. Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:
P = 2 (a + b).
Площадь параллелограмма не зависит от величины его углов, и находится по следующей формуле:
S = a × h.
Параллелограммы часто встречаются в реальной жизни: это грани многих призматических объектов, очертания полей, спортивных площадок или клумб. Форму параллелограммов имеют практически все отделочные материалы: плитка, кафель, гипсокартон, паркет. Такое разнообразие обусловлено тем, что частными случаями параллелограмма являются прямоугольник, ромб и квадрат, формулы для определения периметров и площадей которых аналогичны или выводятся из теоремы Пифагора.
Частные случаи
Ромб — четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Прямоугольник — это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Квадрат — это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
- пять сторон — пентагон;
- шесть — гексагон;
- восемь — октагон;
- двенадцать — додекагон.
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
P = n × a,
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов.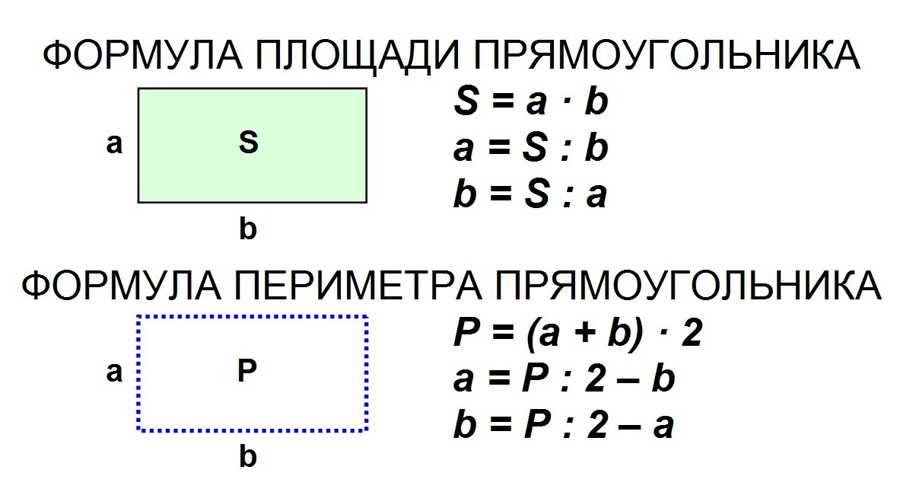 Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
P = 400
Таким образом, нам понадобится 4 м бахромы для отделки платка.
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Площадь прямоугольника. Онлайн калькулятор
|
0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
При помощи данного калькулятора вы можете легко найти площадь прямоугольника (через две стороны, периметр и любую сторону, диагональ и любую сторону, диагональ и синус острого угла между диагоналями, радиус описанной окружности и любую сторону, через диаметр описанной окружности и любую сторону) и получите подробное решение
Укажите известную величину прямоугольника
Две стороныПериметр и любая сторонаДиагональ и любая сторонаДиагональ и синус острого угла между диагоналямиРадиус описанной окружности и любая сторонаДиаметр описанной окружности и любая сторона
| Сторона a |
| Сторона b |
|
|
Как вычислить площадь прямоугольника
Прямоугольник — это четырехугольник, все углы которого прямые
Площадь прямоугольника равна
S = a · b =
Pa — 2a2
2
=
Pb — 2b2
2
=
a√d2 — a2
=
b√d2 — b2
=
d2 · sin α
2
=
a√4R2 — a2
=
b√4R2 — b2
=
a√D2 — a2
=
b√D2 — b2
=
, где
а — сторона прямоугольника
b — сторона прямоугольника
P — периметр прямоугольника
d — диагональ прямоугольника
sin α — синус острого угла между диагоналями
R — радиус описанной окружности прямоугольника
D — диаметр описанной окружности прямоугольника
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона.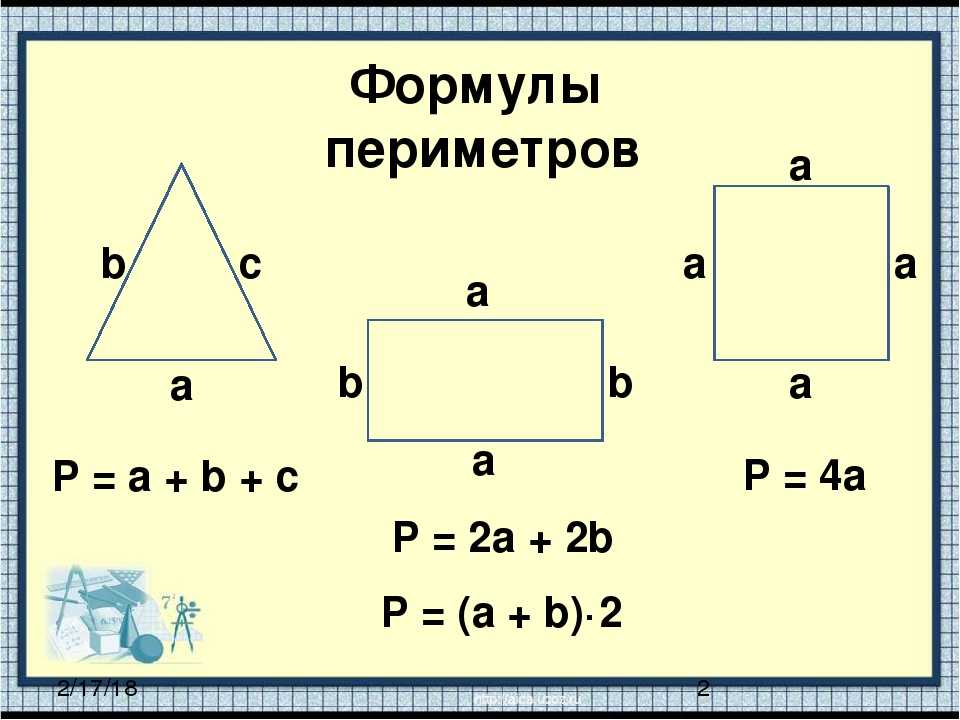 Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
|
Калькулятор вычисления энергии W заряженного конденсатора.  Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
|
Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Калькулятор периметра 📐 — рассчитайте периметр квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции, эллипса…
Быстрая навигация:
- Как рассчитать периметр любой формы?
- Периметр квадрата
- Периметр прямоугольника
- Периметр треугольника
- Длина окружности
- Периметр параллелограмма
- Периметр трапеции
- 0008
- Периметр сектора
- Периметр восьмиугольника
- Где полезен калькулятор периметра?
Как вычислить периметр любой фигуры?
Существуют разные правила расчета периметра различных геометрических фигур. Наш калькулятор периметра поддерживает множество основных фигур, и ниже вы можете прочитать подробную информацию о каждой из них, включая формулу расчета периметра. При выполнении расчетов не забывайте проводить каждое измерение в одних и тех же единицах или преобразовывать их в одни и те же единицы, чтобы получить достоверные результаты.
Наш калькулятор периметра поддерживает множество основных фигур, и ниже вы можете прочитать подробную информацию о каждой из них, включая формулу расчета периметра. При выполнении расчетов не забывайте проводить каждое измерение в одних и тех же единицах или преобразовывать их в одни и те же единицы, чтобы получить достоверные результаты.
Периметр квадрата
Формула для периметра квадрата: сторона x 4 , как показано на рисунке ниже: одно измерение. Для этого даже калькулятор не нужен. Однако он также редко встречается в практических вопросах.
Периметр прямоугольника
Формула периметра прямоугольника: (ширина + высота) x 2 , как показано на рисунке ниже:
Для прямоугольника нужны два измерения — ширина и длина. Убедитесь, что оба значения указаны в одних и тех же единицах измерения, или при необходимости преобразуйте одно из них. Из-за простоты формы измерения легко выполнить, а калькулятор периметра упрощает расчет только при больших числах.
Периметр треугольника
Формула периметра треугольника: сторона а + сторона b + сторона с , но есть много правил, по которым его можно вычислить. Наглядно на рисунке ниже:
Наш калькулятор периметра также поддерживает следующие правила: SAS (сторона, угол, сторона), SSA (сторона, сторона, угол), ASA (угол, сторона, угол) и гипотенуза и сторона Правило прямоугольных треугольников.
Длина окружности
Формула для длины окружности: 2 x π x радиус , но диаметр окружности равен d = 2 x r, поэтому по-другому можно записать число 9.0041 2 х π х (диаметр / 2) . Визуально на рисунке ниже:
Во многих практических ситуациях проще точно измерить диаметр, чем радиус. Кроме того, во многих инженерных схемах по умолчанию указывается диаметр окружности, а не радиус.
Периметр параллелограмма
Формула для периметра параллелограмма (ширина + высота) x 2 , как показано на рисунке ниже:
Периметр параллелограмма рассчитывается по той же формуле, что и прямоугольник, поскольку в обеих фигурах противоположные стороны равны по длине.
Периметр трапеции
Формула периметра трапеции: основание 1 + основание 2 + сторона a + сторона b , как показано на рисунке ниже:
5 9000 трапеция, так как это более сложная форма, у которой все стороны могут иметь разную длину.
Окружность эллипса (овала)
Единой формулы для длины окружности эллипса не существует, так как ее точное вычисление на удивление сложно. Мы используем точный способ его вычисления, который приводит к точному вычислению после бесконечного числа вычислений. Если количество вычислений меньше бесконечности, возникает небольшая ошибка. Он быстро сходится к истинному значению, поэтому мы делаем только несколько шагов.
Сначала калькулятор вычисляет h = (большой радиус — малый радиус) 2 / (большой радиус + малый радиус) 2 . Затем он вычисляет периметр как равный π x (большой радиус + малый радиус) x (1 + h * 0,25 + h 2 * (1/64) + h 3 * (1/256) + h 4 * (25/16384) + h 5 * (49/65536) + h 6 * (441/1048576) .
Формула для периметра сектора: 2 x радиус + радиус x угол x (π / 360) . Визуально на рисунке ниже:
Сектор — это просто часть круга, поэтому формула похожа. Дополнительная сложность возникает из-за необходимости вычислять, какая часть круга приходится на сектор.
Периметр восьмиугольника
Формула периметра правильного восьмиугольника: сторона x 8 , как показано на рисунке ниже:
Это одна из самых простых фигур для вычисления периметра — требуется только одно измерение, а простое умножение на восемь — это все необходимые расчеты. Правильные восьмиугольники можно встретить в технике, садово-парковом искусстве, архитектуре.
Где полезен калькулятор периметра?
Помимо очевидных задач на уроках геометрии или домашних заданий, калькулятор периметра может иметь множество практических применений. Например, в спорте — вы можете решить, что вам нужно ходить или бегать по 10 км в день, чтобы оставаться в хорошей физической форме. Однако что делать, если поблизости нет хороших трасс? Вы можете просто выбрать большое здание или любой прямоугольный квартал или набор кварталов, рассчитать их периметр, а затем разделить на него 10 км, чтобы определить, сколько кругов вам нужно сделать.
Однако что делать, если поблизости нет хороших трасс? Вы можете просто выбрать большое здание или любой прямоугольный квартал или набор кварталов, рассчитать их периметр, а затем разделить на него 10 км, чтобы определить, сколько кругов вам нужно сделать.
Калькулятор также может быть полезен в различных проектах «сделай сам» дома или в саду, в том числе в таких вещах, как украшение дома, рукоделие и т. д. Работа в области машиностроения и некоторых ремесел часто заканчивается необходимостью расчета периметра.
Калькулятор площади прямоугольника
Создано Богной Шик и Ханной Памула, кандидатами наук
Отредактировано Джеком Боуотером
Последнее обновление: 14 сентября 2022 г.
Содержание:
- Что такое прямоугольник?
- Как найти площадь прямоугольника?
- Формулы прямоугольника
- Вычисление прямоугольника: найти A (площадь)
- Вычисление прямоугольника: найти P (периметр)
- Вычисление прямоугольника: найти D (диагональ)
- Золотой прямоугольник
- Свойства прямоугольника
8 формы.
 Является ли квадрат прямоугольником?
Является ли квадрат прямоугольником? - Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
- Прямоугольники
- Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть…
- Часто задаваемые вопросы
Если вам нужно узнать площадь ковра, посылки, экрана телевизора, прямоугольного бассейна или окна, этот калькулятор площади прямоугольника решит вашу проблему в мгновение ока. !
Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить этому прямоугольнику вычислить значения P (периметр) и A (площадь).
Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересует определение прямоугольника, формулы и свойства прямоугольника… Или вы просто хотите узнать, как найти площадь прямоугольника.
Что такое прямоугольник?
Прямоугольник — это четырехугольник с четырьмя прямыми углами . Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же. При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же. При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
Если вы немного знаете латынь, название фигуры обычно многое объясняет. Слово прямоугольник происходит от латинского прямоугольный . Это комбинация rectus (что означает «правильный, прямой») и angulus (угол), так что это может служить простым базовым определением прямоугольника.
Прямоугольник является примером четырехугольника. Вы можете использовать наш четырехугольник калькулятор, чтобы найти площадь других типов четырехугольника.
Как найти площадь прямоугольника?
На изображении выше показан обычный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначим через a и b , а длина диагонали обозначается d .
Если все стороны прямоугольника имеют одинаковую длину, мы называем его квадратом .
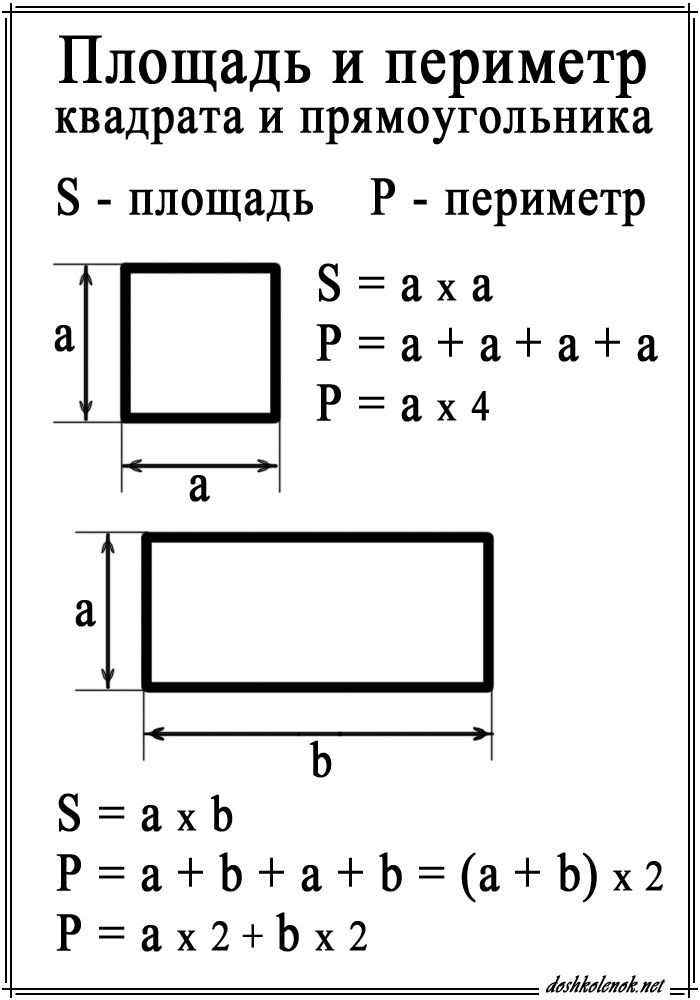
Площадь прямоугольника — это пространство, ограниченное его сторонами или, другими словами, в пределах периметра прямоугольника. Чтобы найти площадь прямоугольника, все, что вам нужно сделать, это умножить стороны прямоугольника a и b :
Площадь = a × b
Формулы прямоугольников
В нашем калькуляторе прямоугольников реализованы следующие формулы:
Для площади прямоугольника :
A = a × bДля периметра прямоугольника :
P = 2 × (a + b)Для диагонали прямоугольника :
d² = a² + b²
d = √(a² + b²)
Расчет прямоугольника: найти A (площадь)
Поскольку мы знаем формулу площади прямоугольника A = a × b , покажем на примере, как можно вычислить это свойство:
- Выберем длину прямоугольника – например,
a = 5 см.
- Определитесь с шириной прямоугольника – например,
b = 6 см. - Умножьте эти два значения:
A = 5 см × 6 см = 30 см². - Площадь прямоугольника 30 см².
Расчет прямоугольника: найти P (периметр)
Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр представляет собой сумму всех сторон фигуры:
P = a + b + a + b
… что можно записать как:
P = 2 × (a + b )
Возьмем для примера тот же прямоугольник:
- Выберем длину прямоугольника –
a = 5 смв нашем случае. - Определите ширину прямоугольника – например,
b = 6 см. - Добавьте эти два значения:
а + b = 5 + 6 = 11 см. - Умножьте результат на 2:
P = 2 × 11 = 22 см. - Поехали! Периметр нашего прямоугольника равен 22 см.
Расчет прямоугольника: найти D (диагональ)
Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника. Вычислим длину диагонали примерного прямоугольника:
Вычислим длину диагонали примерного прямоугольника:
- Выберем длину прямоугольника – например,
а = 5 см. - Определитесь с шириной прямоугольника – например,
b = 6 см. - Вычислите
aв степени двойки:a² = 25 см². - Вычислите
bв степени двойки:b² = 36 см². - Сложите эти два значения:
a² + b² = 25 + 36 = 61 см². - Наконец, извлеките квадратный корень из результата:
d = √(a² + b²) = √61 ~ 7,81 см. - Длина диагонали 7,81 см.
Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область калькулятора прямоугольника. Вы также можете использовать его в обратном порядке — например, для вычисления ширины прямоугольника с известными длиной и периметром.
Золотой прямоугольник
На рисунке выше показан особый тип прямоугольника, называемый золотым прямоугольником (узнайте с помощью нашего калькулятора золотого прямоугольника). Такой прямоугольник удовлетворяет следующему условию:
Такой прямоугольник удовлетворяет следующему условию:
(a + b) / a = a / b = ϕ
, где φ — золотое сечение, равное 1,618. Узнайте больше об этом особом соотношении с помощью нашего калькулятора золотого сечения.
Как вы, вероятно, помните из калькулятора отношений, отношение — это отношение между двумя величинами, часто представленное в виде дроби.
Знаете ли вы, что золотой треугольник можно построить, используя только линейку и циркуль ? Это всего несколько шагов!
- Нарисуй квадрат.
- Проведите линию от середины одной стороны квадрата до противоположного угла. Наш калькулятор средней точки может помочь вам с этим шагом.
- Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как показано на рисунке выше.
- Точка, в которой круг встречается с расширенной стороной квадрата, является следующим углом золотого прямоугольника.
- Найдите последнюю вершину и завершите золотой прямоугольник.

Таадааах! Это было не так сложно, не так ли?
Свойства прямоугольника
Прямоугольники обладают многими интересными свойствами:
- Цикличность – это означает, что все углы лежат на одной окружности.
- Равноугольный – все его углы равны 90 градусам.
- Прямолинейный – его стороны сходятся под прямым углом.
- Две линии отражательной симметрии – вертикальная и горизонтальная через центр.
- Две диагонали, которые делят друг друга пополам . Длину диагонали можно найти по теореме Пифагора.
- Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.
Другие менее известные прямоугольные свойства:
- Пересечение диагоналей — это центр описанной окружности — существует окружность с центром в этой точке, которая проходит через четыре угла.

- В прямоугольнике с разной длиной сторон (попросту говоря, не в квадрате) невозможно провести вписанную окружность.
- Прямые, соединяющие середины сторон прямоугольника, образуют ромб, площадь которого составляет половину площади прямоугольника. Стороны фигуры параллельны диагоналям.
Можно придумать и свои собственные свойства, например, о вращении прямоугольника — по стороне или диагонали, чтобы получился цилиндр или конус соответственно.
Прямоугольник и другие формы. Является ли квадрат прямоугольником?
TL;DR:
- Является ли квадрат прямоугольником? ДА .
- Является ли прямоугольник параллелограммом? ДА .
- Является ли прямоугольник ромбом? В целом – НЕТ. Только если это квадрат (все углы ромба 90 градусов).
- Является ли ромб прямоугольником? В целом – НЕТ. Только если это квадрат (все стороны прямоугольника равны по длине).

- Является ли прямоугольник четырехугольником? ДА , конечно.
- Является ли прямоугольник трапецией? ДА .
Хотите знать, является ли квадрат прямоугольником или прямоугольник параллелограммом? Взгляните на картинку ниже, и у вас больше не должно быть никаких сомнений относительно отношений между четырехугольниками:
Источник: Wikimedia
Как читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к фигуре присоединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция. Таким образом, если фигура находится выше интересующей нас формы, например, квадрата и прямоугольника, мы можем сказать, что:
- Каждый квадрат является прямоугольником , а квадрат является частным случаем прямоугольника .
Для двух других цифр аналогично:
- Каждый прямоугольник является параллелограммом и прямоугольник является частным случаем параллелограмма .

- Каждый прямоугольник является трапецией и прямоугольник является частным случаем трапеции .
Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
Существует множество различных рейтингов, оценивающих страны по площади, населению, уровню образования или лауреатам Нобелевской премии.
Но задумывались ли вы когда-нибудь Кто победит в конкурсе на самую прямоугольную страну? Австралийский геостатистик Дэвид Бэрри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг.
Он выяснил, что самой прямоугольной страной является Египет, тогда как титул «наименее прямоугольной страны в мире» достается Мальдивским островам (впрочем, автор допускает, что расчеты для стран, состоящих из множества мелких островов, могут быть ужасно неверными). Взгляните на таблицу ниже и проверьте первые десять стран, а также наименее прямоугольные.
Ранг | Страна | Круглость | Изображение |
|---|---|---|---|
1 | Египет | 0,955 | |
2 | Ватикан | 0,948 | |
3 | Синт-Мартен | 0,937 | |
4 | Лесото | 0,936 | |
5 | Йемен | 0,928 | |
6 | Гана | 0,924 | |
7 | Македония | 0,921 | |
8 | Кот-д’Ивуар | 0,919 | |
9 | Польша | 0,919 | |
10 | Науру | 0,917 | |
. | |||
169 | США | 0,735 | |
… | |||
206 | Тувалу | 0,240 | |
207 | Маршалловы Острова | 0,201 | |
208 | Мальдивы | 0,018 |
Египет — лидер, но это не должно никого удивлять, проверяя форму этой страны на карте. США находится в середине рейтинга, в основном из-за эксцентричности Аляски и Гавайев. Сбивает с толку то, что 2-я самая прямоугольная страна – Ватикан – одновременно является 4-й страной по круглости, а Польша , 5-е место в классификации округлости, занимает 9-е место в рейтинге прямоугольности.
Как вообще возможно быть прямоугольным и круглым одновременно?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которое может быть неадекватным для сложных или разбросанных форм — и такими примерами обычно являются границы стран, содержащие острые края, маленькие острова или колонии где-то на другой стороне. земного шара.
земного шара.
Если вам интересна эта тема, вы можете ознакомиться с этим объяснением и обсуждением результатов. Кроме того, в калькуляторе кругов вы найдете специальный параграф о круглости стран с аналогичной таблицей и примерами.
Можно подумать, что мир было бы легче рисовать, если бы каждая страна была прямоугольником… Или нет?
Шаблоны прямоугольников
Форма прямоугольника используется во многих периодических шаблонах мозаики. Его можно использовать для стен из кирпича, напольной плитки, тротуара или различной мозаики. Ниже вы найдете несколько популярных шаблонов:
- Укладка в стопку – самый распространенный и простой способ укладки плитки, так как плитка укладывается прямыми линиями.
- Текучая связка – типична для дорожных покрытий, плитки и кирпичной кладки.
- Елочка – с таким рисунком хорошо смотрятся деревянные полы.
- Корзиночное плетение – часто используется для коридоров или дорожек на открытом воздухе.

Конечно, плитка бывает всех форм и размеров – довольно популярны шестиугольные и восьмиугольные с квадратами. Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
Прямоугольники в повседневной жизни: прямоугольное тело, прямоугольный бассейн, прямоугольная скатерть…
Телосложение типа — одна из самых популярных проблем, связанных с прямоугольниками. Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высоту бедер и ввести значения в инструмент. Тогда вы получите информацию о том, какая у вас форма тела.
Например, прямоугольная форма тела определяется как «мальчишеский» тип телосложения — ваши бедра, талия и бюст примерно одного размера. Ваше тело имеет правильные пропорции и спортивный вид.
Удивительно, но нас окружают прямоугольные предметы. Вот почему наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач. Конечно, идеального прямоугольника в реальности не найти, так как он всегда имеет третье измерение; но если оно мало по сравнению с двумя другими измерениями, приближение достаточно хорошее.
Конечно, идеального прямоугольника в реальности не найти, так как он всегда имеет третье измерение; но если оно мало по сравнению с двумя другими измерениями, приближение достаточно хорошее.
Прямоугольные скатерти – учитывая размер вашего стола, вы можете узнать, какая скатерть нужна или сколько кружева или подшивочной ленты вам нужно использовать.
Двери или оконное стекло – шторм или мяч для гольфа разбили ваше оконное стекло? Рассчитайте площадь и оцените стоимость ремонта, учитывая цену за кв.м или кв.м.
Экраны электронных устройств – планшетов, смартфонов, телевизоров – используйте этот калькулятор площади прямоугольника, чтобы оценить, сколько места на стене займет ваш экран – или насколько велик экран телефона, который вы хотите купить.
Доски, зеркала, рамы, холст, листы бумаги, блокноты, конверты, деньги, флажки, прямоугольные бассейны.
 .. Это бесконечный список!
.. Это бесконечный список!
Посмотрите. Можете ли вы найти больше прямоугольных объектов вокруг вас? Что вы можете!
FAQ
Как найти периметр и площадь прямоугольника?
Чтобы найти периметр, нужно сложить все стороны прямоугольника:
P = a + b + a + b
Чтобы найти площадь прямоугольника, нужно умножить меньшую и длинную сторону :
A = a × b
Какова площадь прямоугольника размером 3 фута на 4 дюйма?
Это 144 квадратных дюйма ! Чтобы найти площадь этого прямоугольника, вам нужно:
- Преобразовать фута в дюймы. 3 фута равны 36 дюймам.
- Умножьте на ширину и длину прямоугольника. Площадь равна 4 умножить на 36.
- Проверьте свой результат в нашем калькуляторе площади прямоугольника!
Как определить, является ли фигура прямоугольником?
Фигура является прямоугольником, если:
- Имеет два измерения – длину и ширину.

 Является ли квадрат прямоугольником?
Является ли квадрат прямоугольником?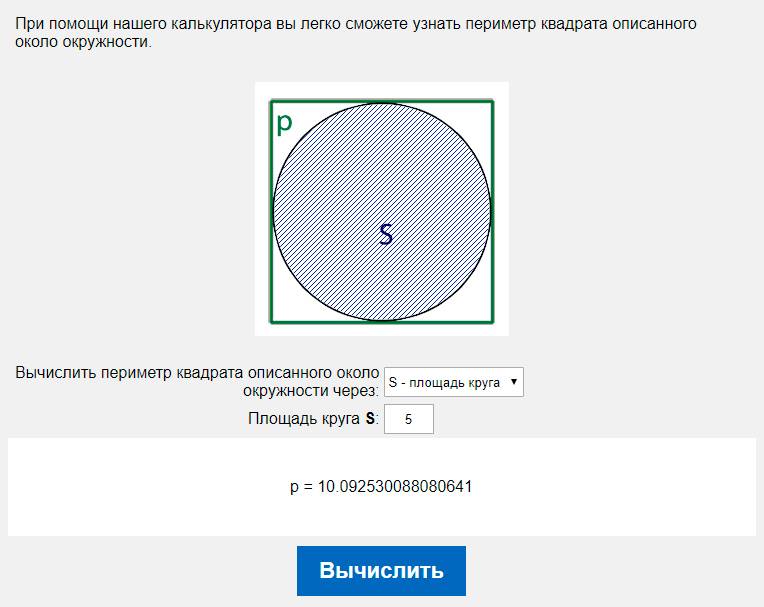


 Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.
Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже. ..
..
 .. Это бесконечный список!
.. Это бесконечный список!