Калькулятор углов: Калькулятор градусов онлайн ° ’ ”.

Содержание

Онлайн калькулятор: Калькулятор выражений с градусами

РаботаИнженерныеКонвертеры

Калькулятор, поддерживающий основные арифметические действия над выражениями с градусами. Создан по запросу пользователя.

Этот калькулятор выполняет арифметические действия над градусами. Как и Арифметика двоичных чисел, технически он сделан на базе калькулятора Математический калькулятор. Сделан был по запросу пользователя Калькулятор .

Вводим выражение с градусами, калькулятор считает. Тонкость тут в форме ввода значений в градусах, ибо символ градуса как-то сложно набрать на клавиатуре. Собственно, вот примеры того, как вводить градусы с их интерпретацией калькулятором:

15 — 15 градусов 0 минут 0 секунд
15.3 — 15 градусов 18 минут 0 секунд (выражение интерпретируется как доли градуса)
15.3′ — 15 градусов 3 минуты 0 секунд (выражение интерпретируется как градусы/минуты)
15. 3’5 — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
15.3’5′ — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
15.3’5» — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
15.3.5 — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3 — 0 градусов 18 минут 0 секунд (выражение интерпретируется как доли градуса)
.3′ — 0 градусов 3 минуты 0 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3.5 — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3’5 — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3’5′ — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
. 3’5» — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)

Несколько вариантов записи, чтобы кому как удобнее было.

Калькулятор действий над градусами

Выражение

Точность вычисления

Знаков после запятой: 2

Результат вычисления (градусы/минуты/секунды)

Результат вычисления (доли градуса)

Ссылка скопирована в буфер обмена

Смежные углы.

Калькулятор онлайн.

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

Найти смежный угол α с углом

градусов.

Смежные углы

Смежные углы – это углы у которых одна сторона является общей, а две другие стороны являются продолжениями одна другой.

Сумма смежных углов равна 180° градусов.
∠AOB + ∠BOC = ∠AOC = 180°
∠AOB = 180° – ∠BOC

Вам могут также быть полезны следующие сервисы

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.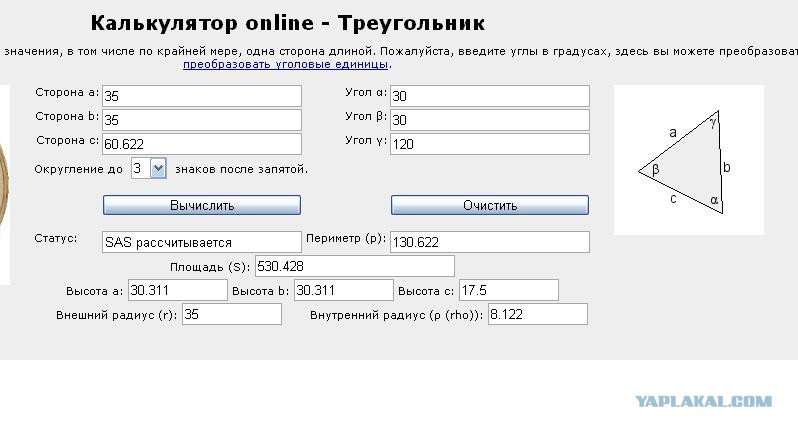

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Калькулятор треугольника

Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.

Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами.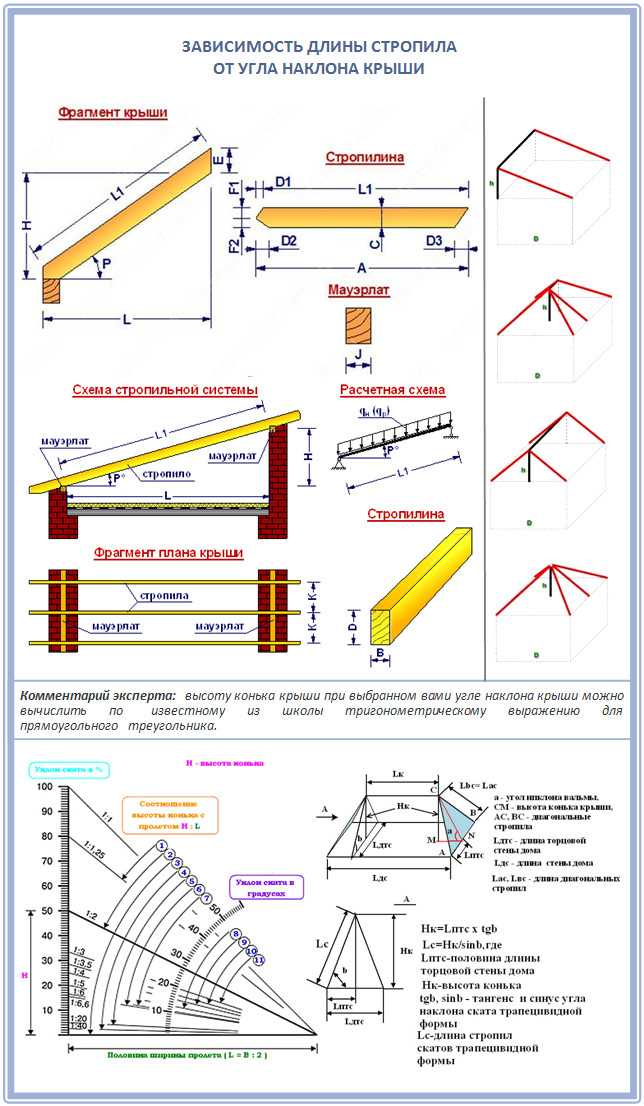 Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины.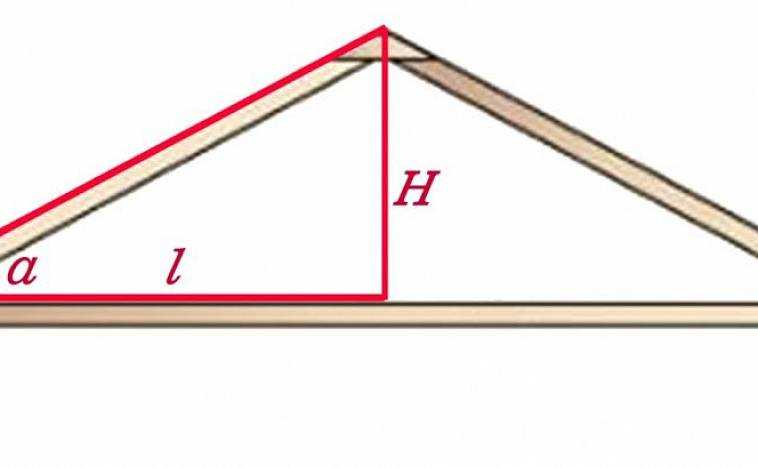 Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.

Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.

Факты, теоремы и законы треугольника

Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.

Площадь треугольника

Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.

Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше.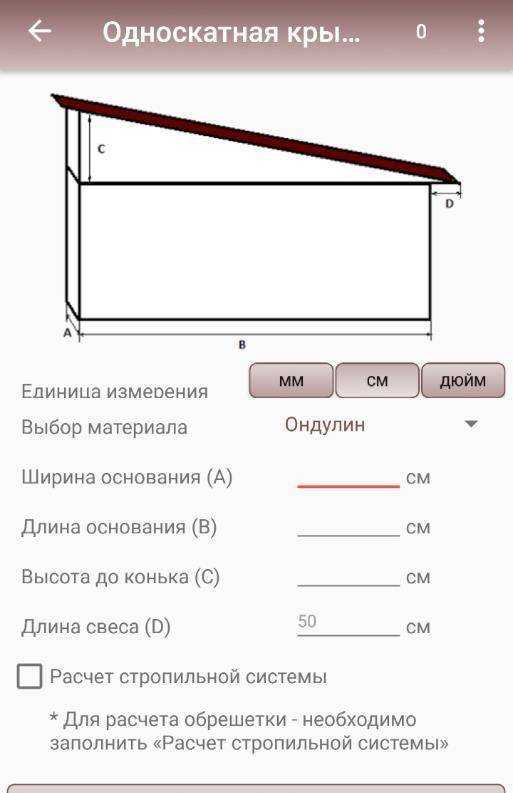 Учитывая а = 9, b = 7 и C = 30°:

Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:

Медиана, внутренний радиус и радиус описанной окружности

Медиана

Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.

Медианы треугольника представлены отрезками m _a , m _b и m _c .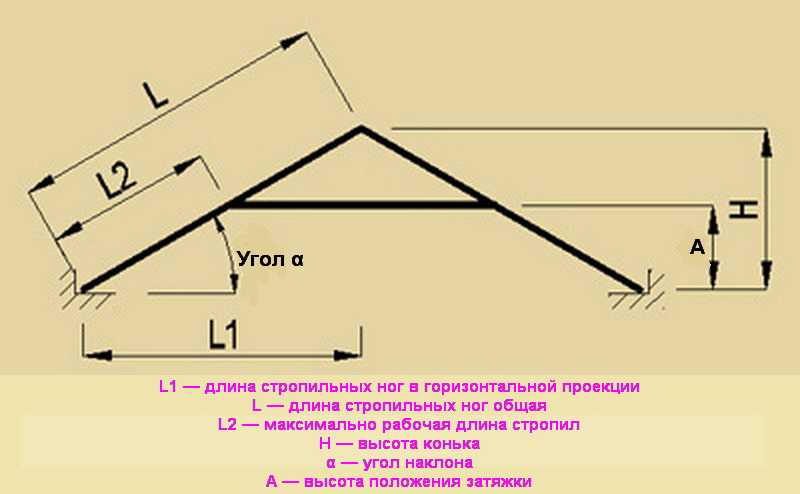 Длину каждой медианы можно рассчитать следующим образом:

Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.

Например, учитывая, что a=2, b=3 и c=4, медиана m _a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.

Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:

внутренний радиус =

с =

а+б+в

где a, b и c — стороны треугольника

Радиус окружности

Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.

Для целей данного калькулятора радиус описанной окружности рассчитывается по следующей формуле:

радиус описанной окружности =

2sin(A)

Где а — сторона треугольника, а А — угол, противоположный стороне а

Хотя сторона а и угол А используются, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.

Калькулятор угла прямоугольного треугольника

Этот калькулятор угла прямоугольного треугольника поможет вам определить, каковы углы прямоугольного треугольника, то есть если вы знаете измерения по крайней мере двух его сторон или хотя бы одной его сторон вместе с его площадью. Продолжайте читать, чтобы узнать о:

Как найти углы прямоугольного треугольника ;
Как пользоваться этим калькулятором ; и
Другие наши калькуляторы треугольников .

Как найти углы прямоугольного треугольника?

Поскольку сумма внутренних углов треугольника составляет 180°, то, если один угол имеет угол, равный 90°, это означает, что оставшиеся два других угла должны иметь в сумме 90°. При этом мы можем сказать, что два оставшихся угла α\alphaα и β\betaβ являются дополнительными углами. В форме уравнения мы выражаем это как:

α+β=90°\альфа + \бета = 90\градусα+β=90°

Итак, если мы знаем один из этих двух углов, как найти недостающие углы прямоугольного треугольника так же просто, как вычесть наш известный угол из 90° 🙂.

С другой стороны, если мы не знаем ни одного из двух углов, мы все равно можем найти их с помощью некоторых основных тригонометрических функций.

Чтобы найти угол α\alphaα, мы можем использовать следующие уравнения:

α=arctan⁡(a/b)\alpha = \arctan(a / b)α=arctan(a/b)
α=arccos⁡(b/c)\alpha = \arccos(b/c)α=arccos(b/c)
α=arcsin⁡(a/c)\alpha = \arcsin(a/c)α=arcsin(a/c)

Для определения угла β\betaβ можно использовать следующие уравнения:

β=arctan⁡(b/a)\beta = \arctan(b/a)β=arctan(b/a)
β=arccos⁡(a/c)\beta = \arccos(a/c)β=arccos(a/c)
β=arcsin⁡(b/c)\бета = \arcsin(b/c)β=arcsin(b/c)

С помощью этих уравнений мы можем видеть, что если у нас есть измерения по крайней мере двух сторон нашего прямоугольного треугольника, мы можем определить, каковы углы прямоугольного треугольника.

Что, если вы знаете размер только одной ноги? Для этого нужно хотя бы знать площадь вашего прямоугольного треугольника, чтобы получить другую сторону вашего треугольника, используя одно из следующих уравнений:

Чтобы найти aaa, зная площадь\текст{площадь}площадь и bbb:

a=2×area/ba = 2 \ times \text{area} / ba=2×area/b

Чтобы найти bbb по заданным \text{area} и aaa:

b=2×area/ab = 2 \times \text{area} / ab= 2×площадь/а

Затем вы можете использовать формулы, которые мы обсуждали ранее, чтобы найти недостающие углы вашего прямоугольного треугольника.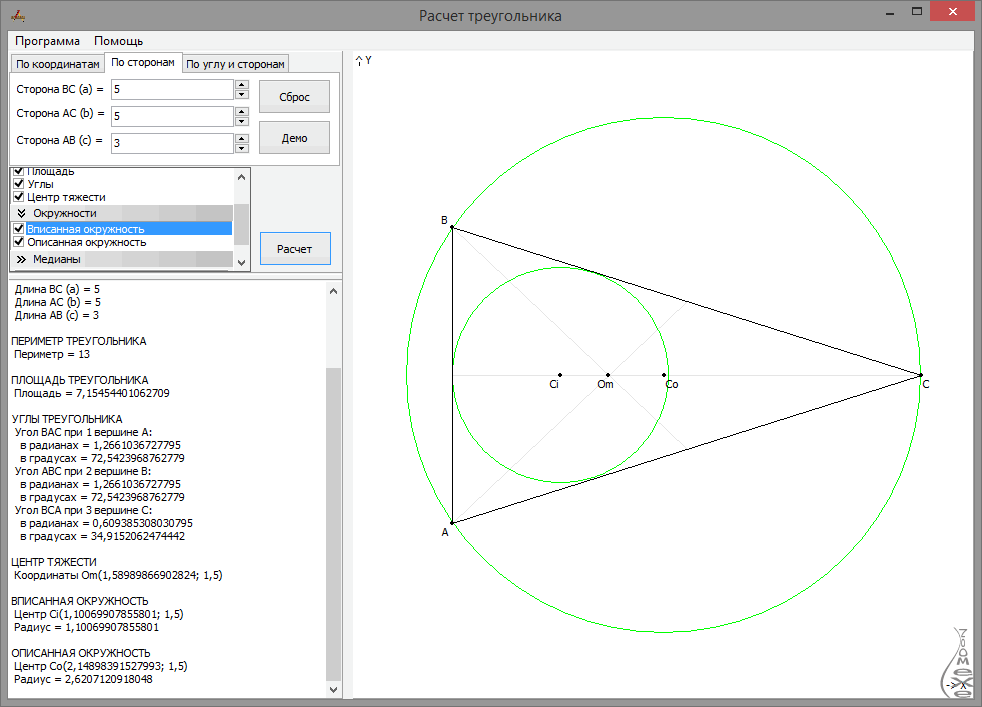

Самое интересное, что мы уже использовали эти уравнения в этом калькуляторе для вашего удобства. Перейдите к следующему разделу этого текста, чтобы узнать, как использовать этот инструмент для расчета угла прямоугольного треугольника 🙂.

🙋 Обратите внимание, что мы не можем найти углы прямоугольного треугольника, если мы знаем только его гипотенузу ccc и его площадь \ текст {площадь}, потому что разные прямоугольные треугольники могут иметь одну и ту же гипотенузу, но с разными площадями.

Как использовать наш калькулятор угла прямоугольного треугольника

Чтобы использовать наш калькулятор угла прямоугольного треугольника, все, что вам нужно сделать, это ввести любые две известные стороны вашего прямоугольного треугольника . Это могут быть измерения двух сторон вашего прямоугольного треугольника (aaa и bbb) или измерения одной стороны и гипотенузы (aaa и ccc или bbb и ccc). Вы также можете ввести одну из сторон вашего треугольника (aaa, bbb или ccc) и площадь\текст{площадь}прямоугольного треугольника .

После этого вы сразу увидите углы вашего прямоугольного треугольника: оба угла α\alphaα и угол β\betaβ. Это так просто!

Если вы хотите еще больше расширить свои знания о треугольниках, вот список других наших калькуляторов треугольников, которые вы можете проверить:

Калькулятор стороны и угла прямоугольного треугольника;
Сторона треугольника;
Отсутствует сторона треугольника;
Длина треугольника;
Градус треугольника;
Сторона и угол треугольника;
Подобные прямоугольные треугольники;
треугольник abc;
Прямоугольный треугольник; и
Проверка подобия прямоугольных треугольников.

Часто задаваемые вопросы

Каковы углы прямоугольного треугольника?

Допустим, прямоугольный треугольник имеет площадь 20 см² и один из его катетов равен 4 см. Чтобы найти углы этого прямоугольного треугольника:

Сначала мы найдем другую сторону треугольника , используя это уравнение: b = 2 × площадь / a , где a = 4 см .